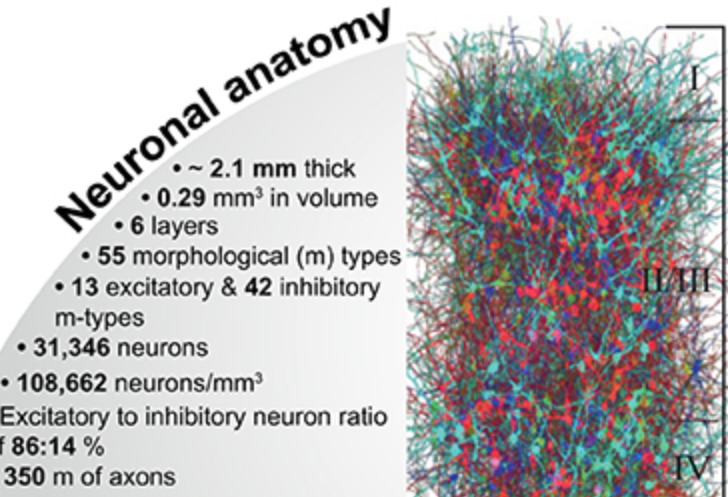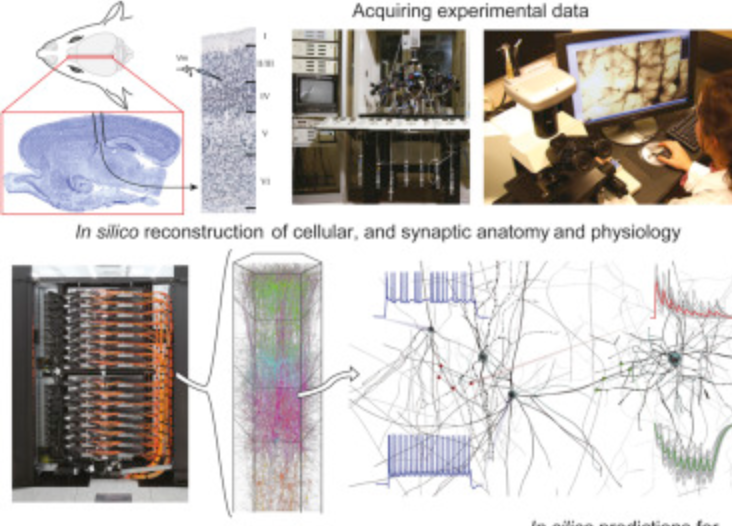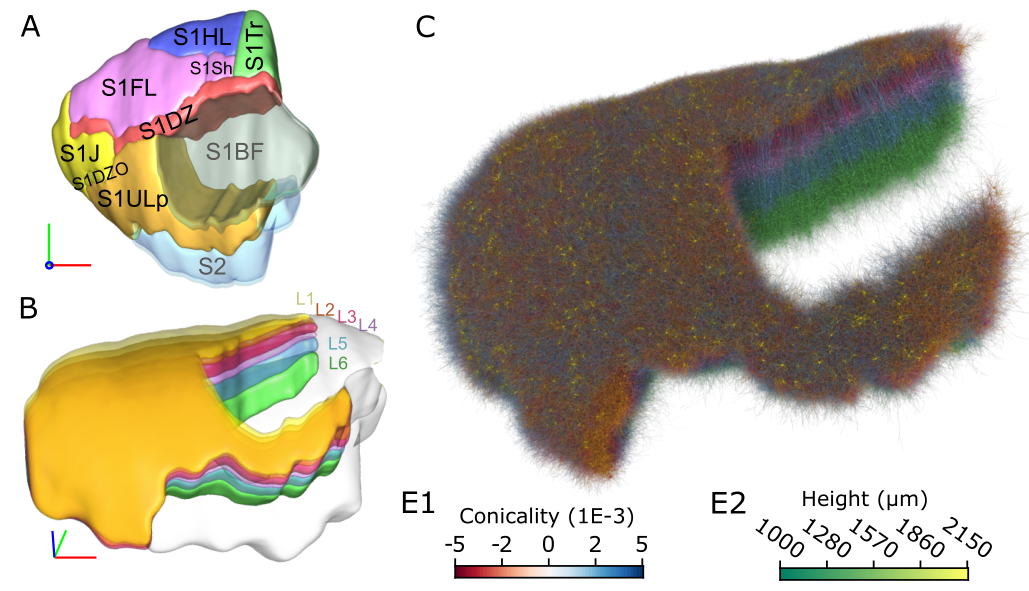
The function of the neocortex is fundamentally determined by its repeating microcircuit motif, but also by its rich, hierarchical, interregional structure with a highly specific laminar architecture. The last decade has seen the emergence of extensive new data sets on anatomy and connectivity at the whole brain scale, providing promising new directions for studies of cortical function that take into account the inseparability of whole-brain and microcircuit architectures. Here, we present a data- driven computational model of the anatomy of non-barrel primary somatosensory cortex of juvenile rat, which integrates whole-brain scale data while providing cellular and subcellular specificity. This multiscale integration was achieved by building the morphologically detailed model of cortical circuitry embedded within a volumetric, digital brain atlas. The model consists of 4.2 million morphologically detailed neurons belonging to 60 different morphological types, placed in the non- barrel subregions of the Paxinos and Watson atlas. They are connected by 13.2 billion synapses determined by axo-dendritic overlap, comprising local connectivity and long-range connectivity defined by topographic mappings between subregions and laminar axonal projection profiles, both parameterized by whole brain data sets. Additionally, we incorporated core- and matrix-type thalamocortical projection systems, associated with sensory and higher-order extrinsic inputs, respectively. An analysis of the modeled synaptic connectivity revealed a highly nonrandom topology with substantial structural differences but also synergy between local and long-range connectivity. Long-range connections featured a more divergent structure with a comparatively small group of neurons serving as hubs to distribute excitation to far away locations. Taken together with analyses at different spatial granularities, these results support the notion that local and interregional connectivity exist on a spectrum of scales, rather than as separate and distinct networks, as is commonly assumed. Finally, we predicted how the emergence of primary sensory cortical maps is constrained by the anatomy of thalamo-cortical projections. A subvolume of the model comprising 211,712 neurons in the front limb, jaw, and dysgranular zone has been made freely and openly available to the community.
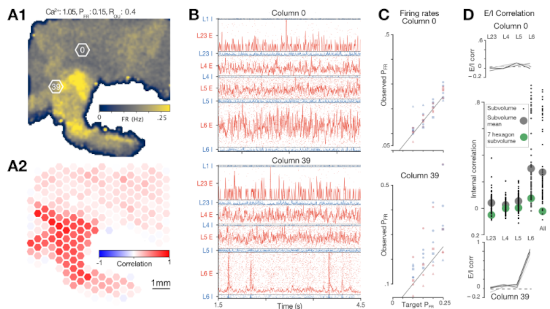
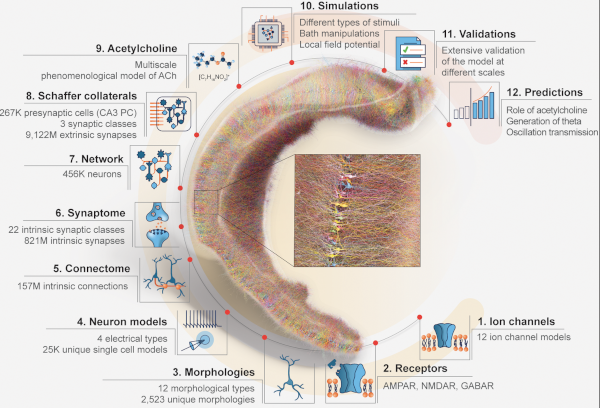
A review paper describing the recent advances in biophysically-detailed modeling. Summarizing the efforts not just of our group, but different labs all around the globe. Written alongside a Minisymposium at SfN 2024.
Understanding the brain requires studying its multiscale interactions from molecules to networks. The increasing availability of large-scale datasets detailing brain circuit composition, connectivity, and activity is transforming neuroscience. However, integrating and interpreting this data remains challenging. Concurrently, advances in supercomputing and sophisticated modeling tools now enable the development of highly detailed, large-scale biophysical circuit models. These mechanistic multiscale models offer a method to systematically integrate experimental data, facilitating investigations into brain structure, function, and disease. This review, based on a Society for Neuroscience 2024 MiniSymposium, aims to disseminate recent advances in large-scale mechanistic modeling to the broader community. It highlights (1) examples of current models for various brain regions developed through experimental data integration; (2) their predictive capabilities regarding cellular and circuit mechanisms underlying experimental recordings (e.g., membrane voltage, spikes, local-field potential, electroencephalography/magnetoencephalography) and brain function; and (3) their use in simulating biomarkers for brain diseases like epilepsy, depression, schizophrenia, and Parkinson's, aiding in understanding their biophysical underpinnings and developing novel treatments. The review showcases state-of-the-art models covering hippocampus, somatosensory, visual, motor, auditory cortical, and thalamic circuits across species. These models predict neural activity at multiple scales and provide insights into the biophysical mechanisms underlying sensation, motor behavior, brain signals, neural coding, disease, pharmacological interventions, and neural stimulation. Collaboration with experimental neuroscientists and clinicians is essential for the development and validation of these models, particularly as datasets grow. Hence, this review aims to foster interest in detailed brain circuit models, leading to cross-disciplinary collaborations that accelerate brain research.
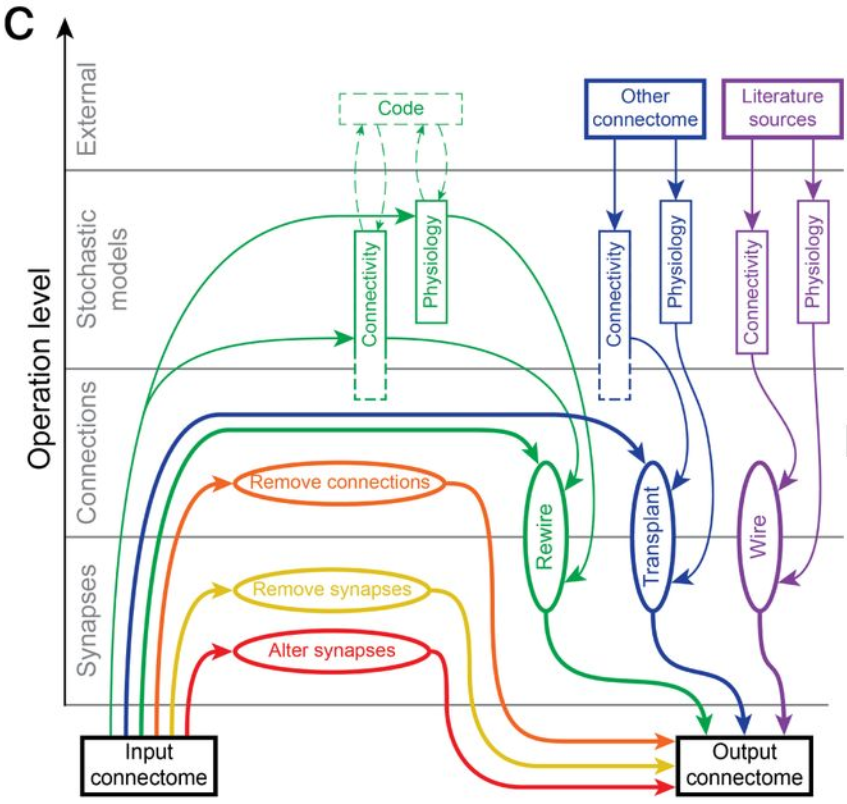
This is an important tool that underlies many of our recent papers. It allows a researcher to systematically and reproducibly wire up even the most detailed model of brain circuitry. Doing so rapidly allows them then to compare and contrast different models of connectivity to understand how connectivity affects activity and - ultimately - function. This is often and easily done in simplified models of brain circuitry. But for more detailed models we run into the complication that also their connectivity is the result of complex algorithms and many parameters that all need to be carefully controlled. This framework enables this.
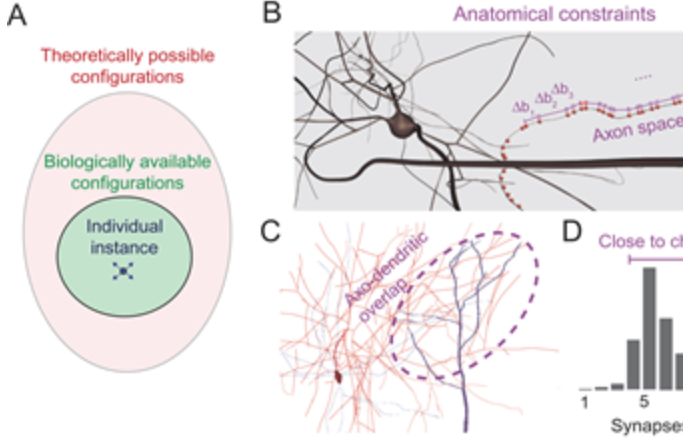
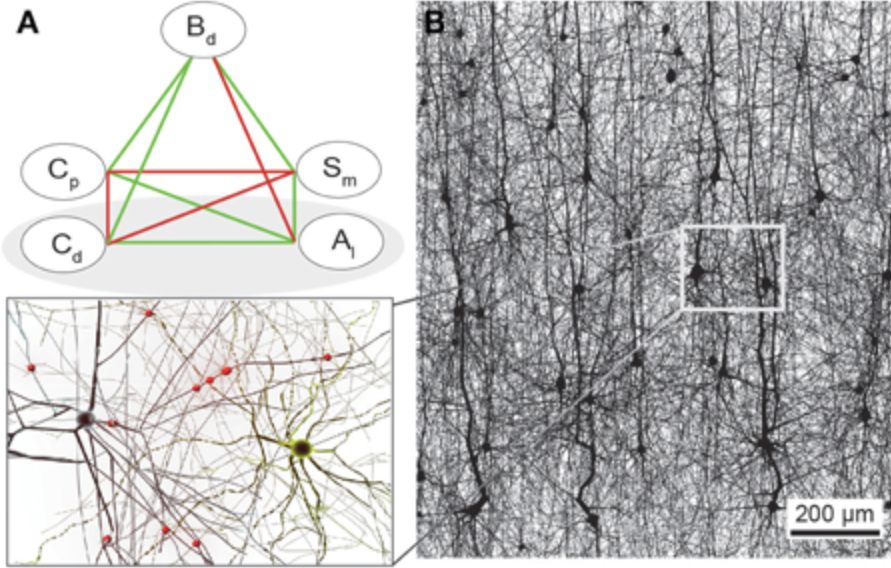
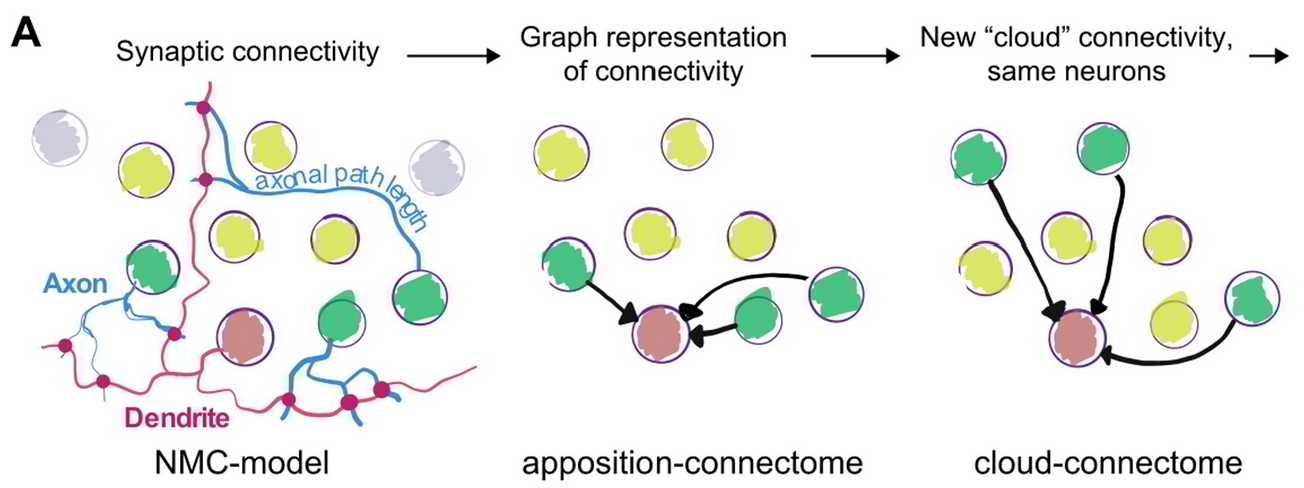
Synaptic connectivity at the neuronal level is characterized by highly non-random features. Hypotheses about their role can be developed by correlating structural metrics to functional features. But to prove causation, manipulations of connectivity would have to be studied. However, the fine-grained scale at which non-random trends are expressed makes this approach challenging to pursue experimentally. Simulations of neuronal networks provide an alternative route to study arbitrarily complex manipulations in morphologically and biophysically detailed models. Here, we present Connectome-Manipulator, a Python framework for rapid connectome manipulations of large-scale network models in SONATA format. In addition to creating or manipulating the connectome of a model, it provides tools to fit parameters of stochastic connectivity models against existing connectomes. This enables rapid replacement of any existing connectome with equivalent connectomes at different levels of complexity, or transplantation of connectivity features from one connectome to another, for systematic study. We employed the framework in a detailed model of rat somatosensory cortex in two exemplary use cases: transplanting interneuron connectivity trends from electron microscopy data and creating simplified connectomes of excitatory connectivity. We ran a series of network simulations and found diverse shifts in the activity of individual neuron populations causally linked to these manipulations.
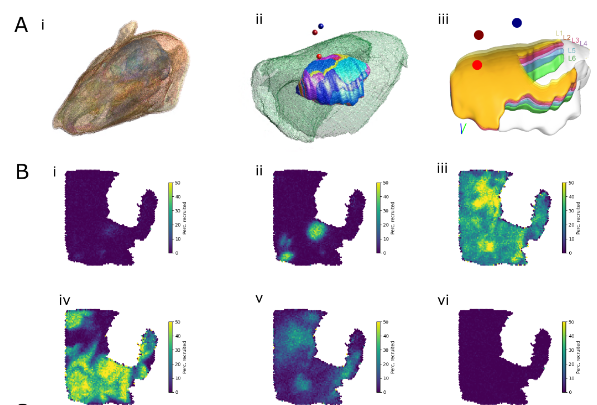
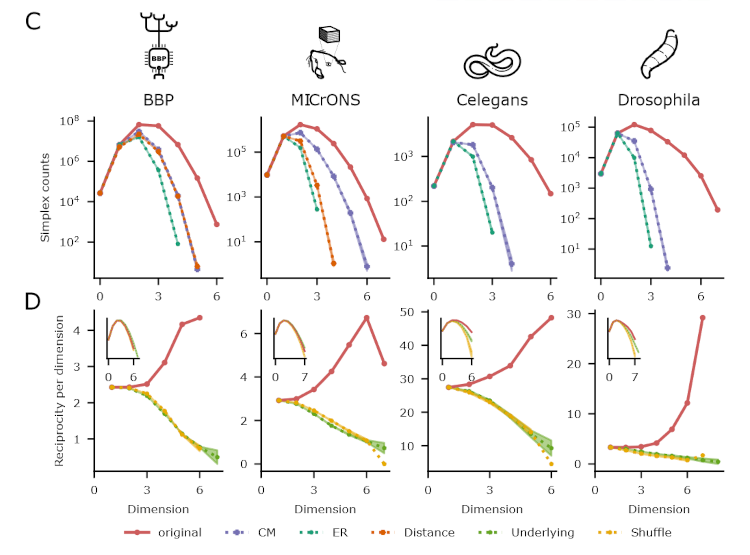
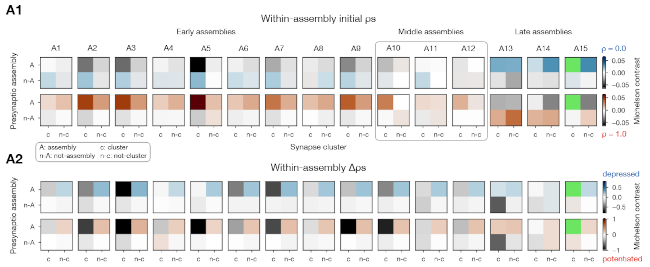
This is the next in a series of papers where we demonstrate that neuronal connectivity at the cellular level is not an amorphous blob, that this matters, and find mathematical ways to describe this. This one is particularly interesting: We analyze both an electron-microscopic connectome with co-registered activity data (MICrONS) and simulations of a morphologically detailed model (BBP) and find the same trends in structure-function relation. We show that higher-order structure of connectivity is crucial to find optimal solutions in a struggle between reliability and efficiency.
The MICrONS dataset is an electron-microscopic (EM) reconstruction of cortical tissue with co-registered functional data. In the field of Connectomics, that is the gold standard of data. Where other experimental approaches can only ever sample tiny fractions of the millions of connections that are present in even small volumes, EM provides a dense reconstruction.
Existing analyses of the dataset were able to confirm the trends that had been proposed based on other experimental approaches. But we wanted to go further and make the most out of this amazing dataset.
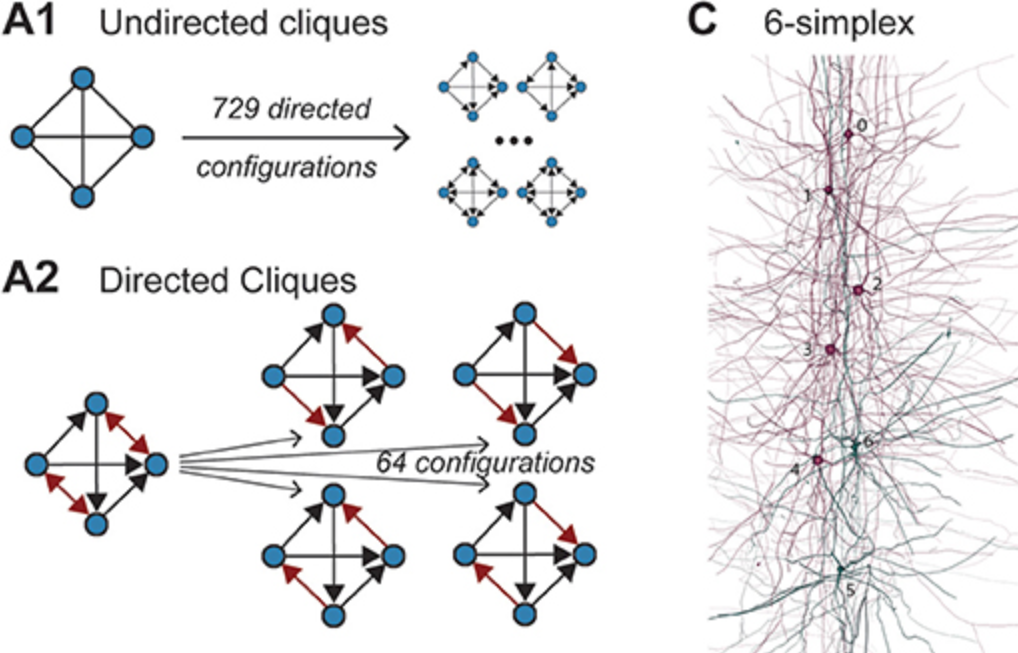
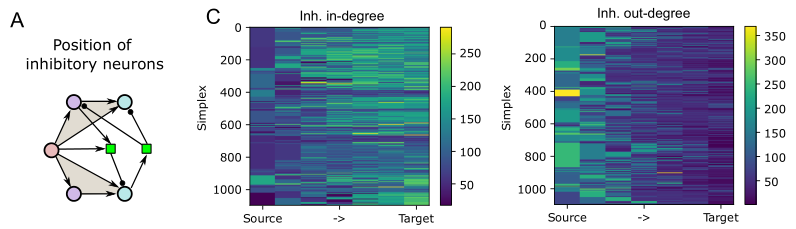
We analyzed the higher-order structure of the graph representing the connectivity between neurons. We first confirmed our earlier predictions that membership in directed simplices, large directed motifs, increases correlations of activity. Wecond, we found that the simplices form a divergent feed-forward network. Third, we found that inhibition is structured by this higher-order feed-forward network, i.e., inhibitory neurons target neurons at specific locations of the network. Fourth, we found that disinhibition, mediated by a group of inhibitory-to-inhibitory specialists, is also structured by the higher-order feed-forward network.
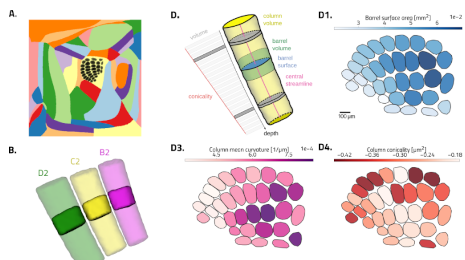
Flat mapping, i.e. generating 2d coordinates for brain voxels is commonly just assumed to happen. But remarkably little is written about how to do it, how to do it properly, and what makes a good flat map in the first place. We describe what we think is an optimal flattening algorithm and present the results.
Along the way, we also demonstrate how certain advantageous properties of flat maps lead to really exciting applications for them.
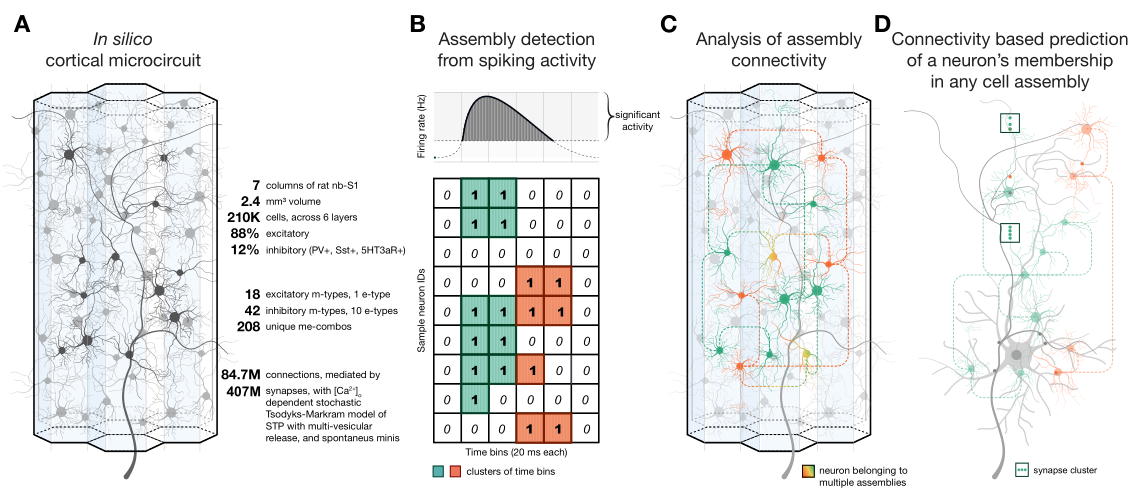

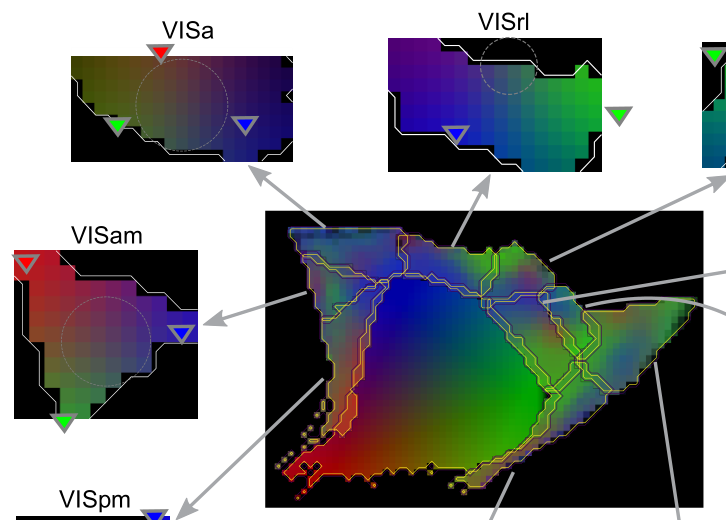
The brain comprises several anatomically clearly separated structures. This parcellation is often extended into the isocortex, where border demarcations are less clear due to its relatively homogeneous structure. Yet, established parcellation schemes exist, based on anatomical, physiological or functional differences. Here, we derive a parcellation scheme based purely on connectomics, that is, the spatial structure of long-range synaptic connections within the cortex. To that end, we analyze a publicly available dataset of average mouse brain connectivity, and split the isocortex into disjunct regions. Instead of clustering connectivity based on similarity or modularity, our scheme is inspired by methods that split sensory cortices into subregions where gradients of neuronal response properties, such as the location of the receptive field, reverse. We developed a method to calculate comparable gradients from voxelized brain connectivity data and automatically detect reversals in them. This approach better respects the known presence of functional gradients within brain regions than clustering-based approaches. Placing borders at the reversals resulted in a parcellation into 41 subregions that differs significantly from an established scheme in nonrandom ways, but is comparable in terms of the modularity of connectivity between regions. It revealed unexpected trends of connectivity, such a a tripartite split of somato-motor regions along an anterior to posterior gradient. The method can be readily adapted to other organisms and data sources, such as human functional connectivity.
PLOS ONE
We are trying to find out how local synaptic connectivity shapes the function of a neural circuit. In this case, in terms of the ability of a circuit to encode information that is useful for a simple classification task. To that end, our approach is as follows: In a detailed microcircuit model, find groups of neurons that differ significantly in how they are connected locally and to the rest of the network. Then correlate these differences with the usefulness of their spike trains for classification of input patterns. Surprisingly, we find that everything depends on exactly how the classification is performed: With established methods, one group of neurons (choristers) performs well, with a new topology-based method we developed, other neurons (soloists) perform better.
In motor-related brain regions, movement intention has been successfully decoded from in-vivo spike train by isolating a lower-dimension manifold that the high-dimensional spiking activity is constrained to. The mechanism enforcing this constraint remains unclear, although it has been hypothesized to be implemented by the connectivity of the sampled neurons. We test this idea and explore the interactions between local synaptic connectivity and its ability to encode information in a lower dimensional manifold through simulations of a detailed microcircuit model with realistic sources of noise. We confirm that even in isolation such a model can encode the identity of different stimuli in a lower-dimensional space. We then demonstrate that the reliability of the encoding depends on the connectivity between the sampled neurons by specifically sampling populations whose connectivity maximizes certain topological metrics. Finally, we developed an alternative method for determining stimulus identity from the activity of neurons by combining their spike trains with their recurrent connectivity. We found that this method performs better for sampled groups of neurons that perform worse under the classical approach, predicting the possibility of two separate encoding strategies in a single microcircuit.
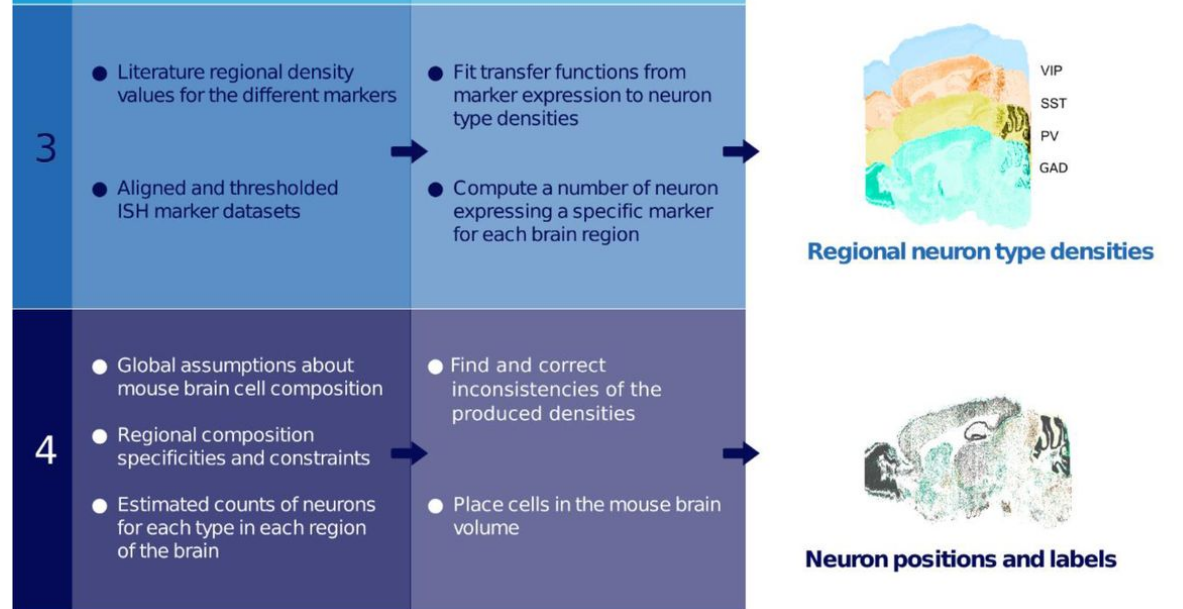
The mouse brain contains a rich diversity of inhibitory interneuron types that have been characterized by their patterns of gene expression. However, it is still unclear how these cell types are distributed across the mouse brain. We developed a computational method to estimate the densities of different interneuron types across the mouse brain. Our method allows the unbiased integration of diverse and disparate datasets into one framework to predict interneuron densities for uncharted brain regions. We constrained our estimates based on previously computed brain-wide neuron densities, gene expression data from in situ hybridization image stacks together with a wide range of values reported in the literature. Using constrained optimization, we derived coherent estimates of cell densities for the different interneuron types. We estimate that 20.3% of all neurons in the mouse brain are inhibitory. Among all inhibitory neurons, 18% predominantly express parvalbumin (PV), 16% express somatostatin (SST), 3% express vasoactive intestinal peptide (VIP), and the remainder 63% belong to the residual GABAergic population. We find that our density estimations improve as more literature values are integrated. Our pipeline is extensible, allowing new cell types or data to be integrated as they become available. The data, algorithms, software, and results of our pipeline are publicly available and update the Blue Brain Cell Atlas. This work therefore leverages the research community to collectively converge on the numbers of each cell type in each brain region.
Obtaining a global understanding of the cellular composition of the brain is a very complex task, not only because of the great variability that exists between reports of similar counts but also because of the numerous brain regions and cell types that make up the brain. Previously, we presented a model of a cell atlas, which provided an estimate of the densities of neurons, glia and their subtypes for each region in the mouse brain. Here, we describe an extension of this model to include more inhibitory neuron types. We collected estimates of inhibitory neuron counts from literature and built a framework to combine them into a consistent cell atlas. Using brain slice images, we also estimated inhibitory neuron density in regions where no literature data are available. We estimated that in the mouse brain 20.3% of all neurons are inhibitory. Among all inhibitory neurons, 18% predominantly express parvalbumin (PV), 16% express somatostatin (SST), 3% express vasoactive intestinal peptide (VIP), and the remainder 63% belong to the residual GABAergic population Our approach can be further extended to any other cell type and provides a resource to build tissue-level models of the rodent brain.
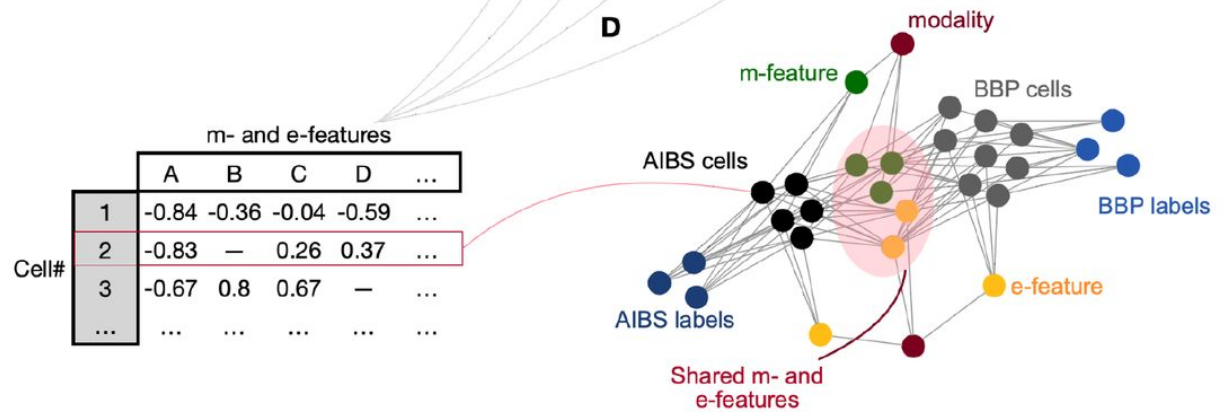
Knowledge of the cell-type-specific composition of the brain is useful in order to understand the role of each cell type as part of the network. Here, we estimated the composition of the whole cortex in terms of well characterised morphological and electrophysiological inhibitory neuron types (me-types). We derived probabilistic me-type densities from an existing atlas of molecularly defined cell-type densities in the mouse cortex. We used a well-established me-type classification from rat somatosensory cortex to populate the cortex. These me-types were well characterized morphologically and electrophysiologically but they lacked molecular marker identity labels. To extrapolate this missing information, we employed an additional dataset from the Allen Institute for Brain Science containing molecular identity as well as morphological and electrophysiological data for mouse cortical neurons. We first built a latent space based on a number of comparable morphological and electrical features common to both data sources. We then identified 13 morpho-electrical clusters that merged neurons from both datasets while being molecularly homogeneous. The resulting clusters best mirror the molecular identity classification solely using available morpho-electrical features. Finally, we stochastically assigned a molecular identity to a me-type neuron based on the latent space cluster it was assigned to. The resulting mapping was used to derive inhibitory me-types densities in the cortex.
The computational abilities of the brain arise from its organisation principles at the cellular level. One of these principles is the neuronal type composition over different regions. Since computational functions of neurons are best described by their morphological and electrophysiological properties, it is logical to use morpho-electrically defined cell types to describe brain composition. However, characterizing morpho-electrical properties of cells involve low-throughput techniques not very well suited to scan the whole brain. Thanks to recent progress on transcriptomic and immuno-staining techniques we are now able to get a more accurate snapshot of the mouse brain composition for molecularly defined cell types.How to link molecularly defined cell types with morpho-electrical cell types remains an open question. Several studies have explored this problem providing valuable three-modal datasets combining electrical, morphological and molecular properties of cortical neurons. The long-term goal of the Blue Brain Project (BBP) is to accurately model the mouse’s whole brain, which requires detailed biophysical models of neurons. Instead of going through the time-consuming process of producing detailed models from the three-modal datasets, we explored a time-saving method. We mapped the already available detailed morpho-electrical models from the BBP rat dataset to cells from a three-modal mouse dataset. We thus assigned a molecular identity to the neuron models allowing us to populate the whole mouse cortex with detailed neuron models.
Nature Communications
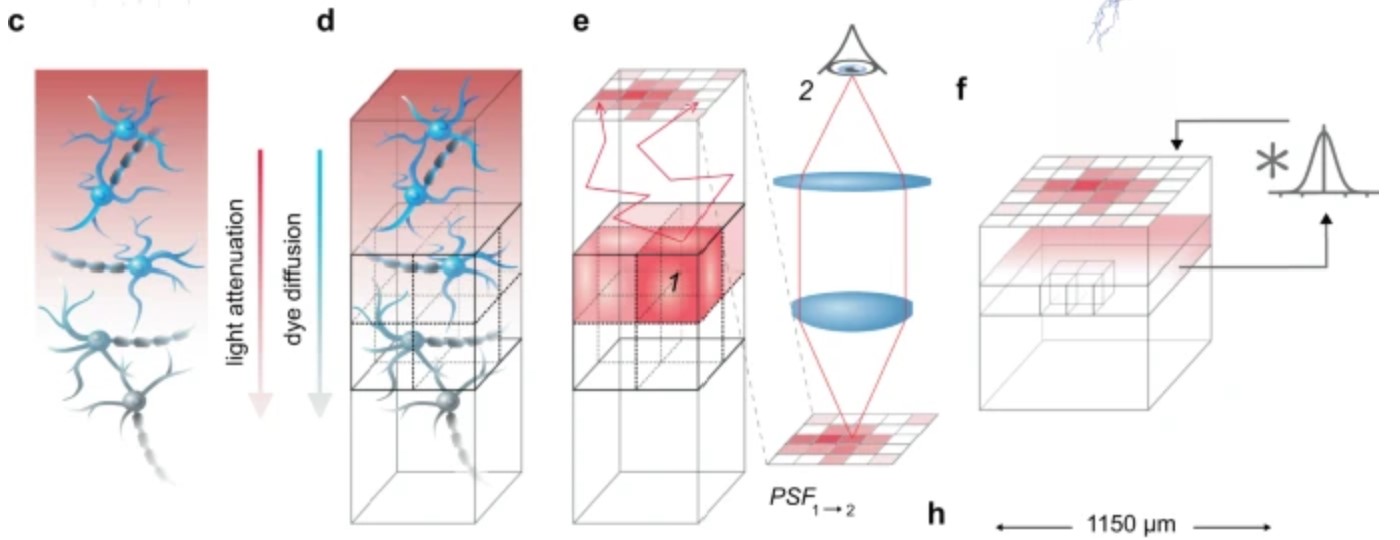
Voltage-sensitive dye imaging (VSDI) is a powerful technique for interrogating membrane potential dynamics in assemblies of cortical neurons, but with effective resolution limits that confound interpretation. To address this limitation, we developed an in silico model of VSDI in a biologically faithful digital reconstruction of rodent neocortical microcircuitry. Using this model, we extend previous experimental observations regarding the cellular origins of VSDI, finding that the signal is driven primarily by neurons in layers 2/3 and 5, and that VSDI measurements do not capture individual spikes. Furthermore, we test the capacity of VSD image sequences to discriminate between afferent thalamic inputs at various spatial locations to estimate a lower bound on the functional resolution of VSDI. Our approach underscores the power of a bottom-up computational approach for relating scales of cortical processing.
biorXiv
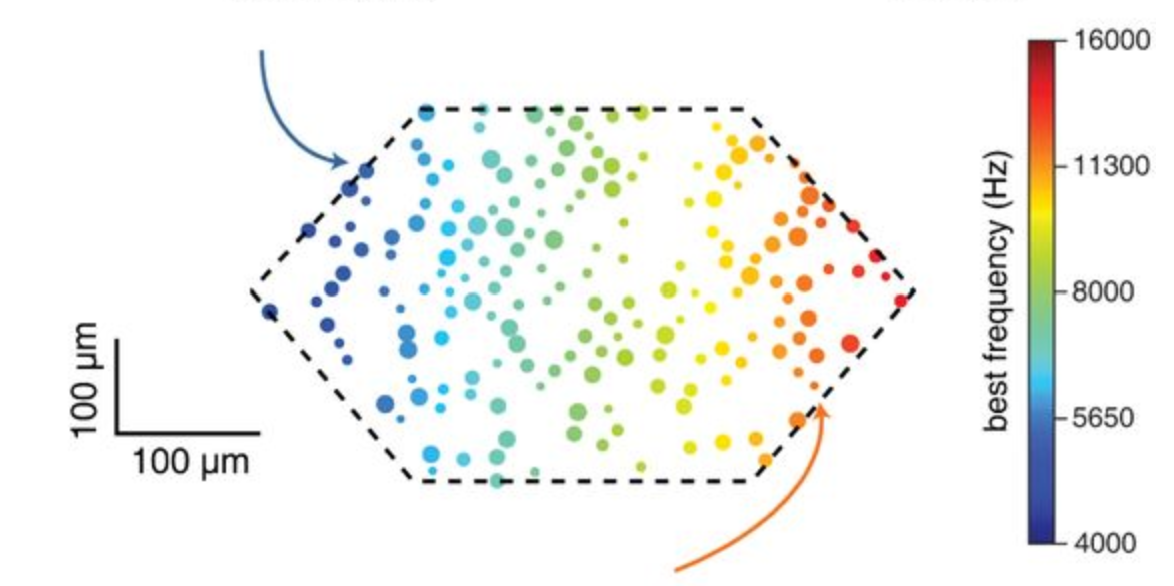
The nervous system is notorious for its strong response evoked by a surprising sensory input, but the biophysical and anatomical underpinnings of this phenomenon are only partially understood. Here we utilized in-silico experiments of a biologically-detailed model of a neocortical microcircuit to study stimulus specific adaptation (SSA) in the auditory cortex, whereby the neuronal response adapts significantly for a repeated (“expected”) tone but not for a rare (“surprise”) tone. SSA experiments were mimicked by stimulating tonotopically-mapped thalamo-cortical afferents projecting to the microcircuit; the activity of these afferents was modeled based on our in-vivo recordings from individual thalamic neurons. The modeled microcircuit expressed naturally many experimentally-observed properties of SSA, suggesting that SSA is a general property of neocortical microcircuits. By systematically modulating circuit parameters, we found that key features of SSA depended on synergistic effects of synaptic depression, spike frequency adaptation and recurrent network connectivity. The relative contribution of each of these mechanisms in shaping SSA was explored, additional SSA-related experimental results were explained and new experiments for further studying SSA were suggested.